A bolygóműves sebességváltók

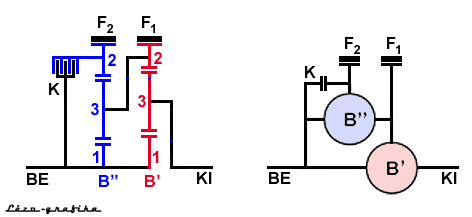
Mint szó volt róla, az átkötött bolygómű átkötő eleme lehet egy kikötött bolygómű. Ennek elvi vázlata itt látható:

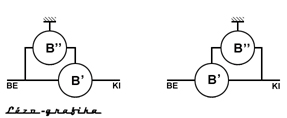Példaként vegyünk két egyszerű, P(P)N típusú bolygóművet, melyeket az alábbi rajz szerint kötöttünk össze. Ennek az összetett bolygóműnek a "képlete": P'x1 (P)'y N'2 + P"1x (P)"2 N"0 , ahol x jelzi a bemenő tengelyt, y a kimenőt, a 0 a befékezett elemet, az arab számok az összeköttetés sorszámát. Esetünkben az egyik összeköttetés a P"1x és a P'x1 napkerék között létesült, a másik a (P)"2 forgattyús kar az N'2gyűrűs kerék között..
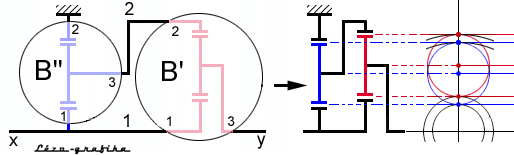A fokozat áttételét először grafikusan állapítjuk meg. Mivel két bolygóműről van szó, a Kutzbach féle szerkesztést kétszer kell elvégezni. Célszerű (de nem szükségszerű) először a kikötött (kék színű) bolygóművel kezdeni. Itt a gyűrűkerék fordulatszáma zérus. Vegyük fel a bemenő tengely fordulatszámához tartozó pillanatnyi kerületi sebesség 1 vektorát, ennek végpontját összekötjük az 2 vektor végpontjával (zérus!).

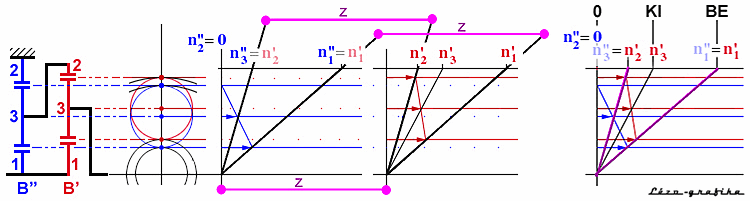
A ferde egyenes a 3 vonalon kimetszi a kikötött bolygómű forgattyújának pillanatnyi kerületi sebességét. Mindkét tengely fordulatszámát fekete vonallal kivetítjük az n egyenesre. A bolygóművek kapcsolódásából következik, hogy az így kapott két fordulatszám megegyezik a másik bolygóműmegfelelő tengelyeinek a fordulatszámával: n"3 = n'2 és n"1 = n'1. Ezt a két fordulatszámot (a fordulatszámot modellező "emelőkart" - ha emlékszünk a mechanikai modellre) átmásoljuk a Z távolságra lévő másik ábrába. Ezek ott  az 1 és 2 egyenesen kimetszik az oda tartozó sebességvektorok végpontját. A két végpontot összekötve, megkapjuk a harmadik kerületi sebesség vektorát, a 3 forgattyújét. Ennek végpontját kivetítve a fordulatszámok egyenesére, megkapjuk az n'3 (kimenő) fordulatszámot. Természetesen nincs értelme a két bolygóműhöz tartozó szerkesztést külön-külön ábrán elvégezni: a harmadik rajzon az előző két szerkesztés összevontan látható.

Emlékezve a mechanikai modellre, itt is érzékelhető a két bolygómű vektorainak összefüggése. Akármelyik emelőkar dőlését megváltoztatjuk, a hozzájuk tartozó vektorok együtt nyúlnak vagy rövidülnek mindkét bolygóműben.

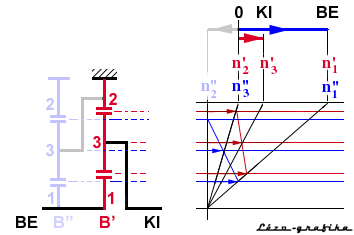Egyébként az így kapott diagramról az előző fejezetben tárgyalt kikötött bolygómű áttétele is kiolvasható: az  n'2fordulatszámot   vesszük zérusnak, azaz onnan mérjük a ki- és a bemenő tengelyek fordulatszámát: a két tengely "fordulatszám-vektorának" aránya, azaz az áttétel ugyanakkora.

Ez a körülmény is arra mutat rá, hogy a két bolygómű közül akármelyiket kiköthetjük, két - egymástól különböző - áttételt kapunk. Valóban, ha megteremtjük ennek a lehetőségét, azaz mindkét bolygóműhöz alkalmazunk féket, akkor kétfokozató váltóművet kapunk (az elmaradhatatlan tengelykapcsoló persze egy harmadik - a direkt - fokozat kapcsolását teszi lehetővé).

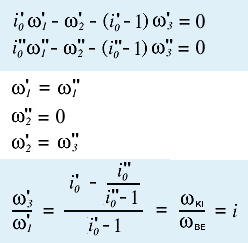Az áttételt természetesen analitikus módszerrel is meghatározhatjuk. Ehhez kétszer kell felírni a kinematikai alapegyenletet, azon kívül az egyenletrendszer megoldásához még további három "egyenletecskére" van szükség, melyek a két bolygómű kapcsolatát, illetve a "felesleges" szabadságfok lekötését írja le. Az egyenletrendszert úgy oldjuk meg, hogy az egyenlet egyik oldalára kerüljön a ki-, illetve a bemenő tengely szögsebességének a hányadosa, a másik oldalra pedig a két alapáttétel.

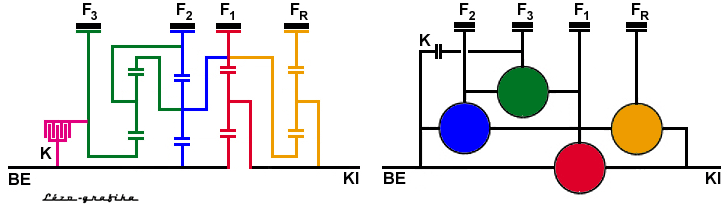
A tisztán bolygóművekből álló sebességváltókban, így például az alább látható klasszikus Wilson-váltóban még több bolygómű található. A váltó "képlete":

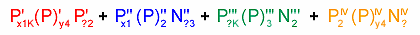ahol a ? kérdőjel a fékezési lehetőségeket jelzi (természetesen egyidejűleg csak egy elemet szabad fékezni, azaz csak egy kérdőjel helyére lehet 0-t írni). A K a tengelykapcsolóval való rövidrezárás lehetőségét jelzi. (Mint látható, a 2-es kapcsolat például mind a négy bolygóművet összeköti.) 

Az ilyen összetett bolygómű úgy jön létre, hogy minden újabb bolygómű úgy kapcsolódik az előzőekhez, hogy három tengelye közül kettő "rá van kötve" a már ott lévő tengelyek közül valamelyik kettőre. (Az összekötések variálhatósága meglehetősen nagy!) Így azután lehetséges, hogy például egy átkötött bolygóműnek az átkötő eleme szintén bolygóművel átkötött másik bolygómű. Ilyenkor három bolygómű van kapcsolatban egymással. Ez a helyzet például a Wilson-váltó harmadik fokozatában is, azaz az F3 fék működtetésekor. Ekkor a piros, a kék és a zöld bolygómű vesz részt a hajtásban. (A sárga bolygómű a hátramenet kapcsolására szolgál.)

A harmadik fokozat áttételének grafikus meghatározását mutatja a mellékelt ábra. Mivel mindhárom bolygómű geometriai mérete azonos, ezét csak három egyenes látható a kerületi sebességek vektorai számára. 
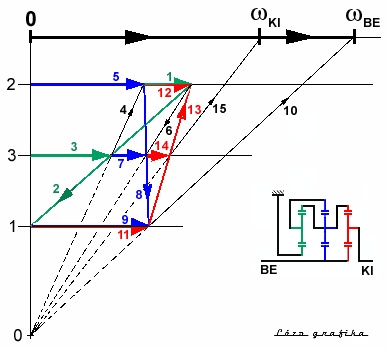A szerkesztést itt is célszerű a kikötött (zöld) bolgyóművel kezdeni. Első lépésként vegyünk fel egy tetszőleges hosszúságú vektort a zöld gyűrűkeréknél (1). Innen húzzunk  egyenest a zöld napkerékhez (2). Ez kimetszi a zöld forgattyúkar vektorát, amit berajzolunk (3). Mivel ez együtt forog a kék bolygómű gyűrűkerekével, a sugárral kivetítjük oda (4), s így megkapjuk annak sebességvektorát (5). Tudjuk, hogy a zöld gyűrűkerék viszont együtt forog  a kék forgattyúval, ezért a sugárral levetítjük (6) a hozzá tartozó vektorhosszat, s megrajzoljuk a vektort (7). A két ismert kék vektor végpontján átfektetett egyenes (8) kimetszi a kék napkerék sebességvektorát (9). Mivel ez egyben a bemenő tengely szögsebességét is megadja, ezért azt kivetítjük a szögsebességek egyenesére (10). Most áttérünk a harmadik (piros) bolygóműre, melynek napkereke együtt forog a kék napkerékkel, kerületi sebességük tehát egyforma (11), gyűrűkereke viszot együtt forog a zöld gyűrűkerékkel, a sebességvektora tehát szintén ismert (12). E két vektor végpontját összekötő egyenes kimetszi (13) a piros forgattyú vektorának hosszát (14). Mivel a piros forgattyús tengely egyben a kimenő tengely is, ezért az utoljára kapott vektort is kivetítjük a szögsebességek egyenesére (15). A két szögsebesség hosszát összevetve megkapjuk az áttételt. 

Ha  további sebességváltó-típusokkal akar megismerkedni, akkor oldja meg a példákat.

Befejezésül néhány szót az egyesített bolygóműről. Ha két vagy több bolygóművet összekötünk (két-két tengelyük összekapcsolásával), azaz "összetett bolygóművet" hozunk létre, akkor előfordulhat, hogy két, egymással összekötött fogaskerék átmérője azonos. 
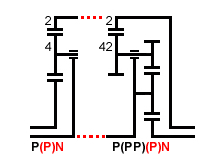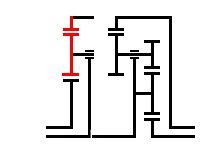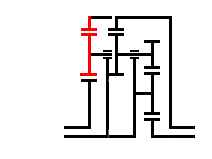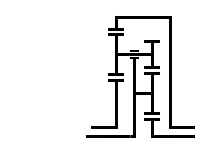Ilyenkor két fogaskereket megtakaríthatunk, ha egyesítjük azokat, amint az itt látható. Eredetileg a P(P)N és egy P(PP)P)N egyszerű bolygóművet kötöttünk össze, de a számítások eredményeként az jött ki, hogy a két gyűrűkerék, s a velük kapcsolódó napkerekek átmérője lehet egyforma. Ezeket "összetolva" olyan bolygóművet kapunk, aminek négy kivezetett tengelye van, azaz eggyel több, mint az egyszerű bolygóműnek. Az egyesített bolygóműre a Kutzbach-féle szerkesztés könnyen elvégezhető, az analitikus elemzéshez azonban előbb "szét kell szedni" a bolygóművet, hogy felírhassuk a szükséges egyenleteket. Ha olyan bolygóművel találkozunk, amelynek öt kivezetett (kivezethető) tengelye van, akkor tudni kell, hogy az három bolygómű egyesítésével jött létre. 

Egyesített bolygóműveket előszeretettel alkalmaznak hidromechanikus váltóművekhez (például a fenti a FORD-O-MATIC-ban jelent meg először).

Amint arról korábban volt szó, egy egyszerű bolygóművel hat áttételt (fokozatot) lehet megvalósítani attól függően, hogy a három tengely közül melyiket fékezzük, melyik a bemeneti, melyik a kimeneti tengely. Néhány sikertelen próbálkozás után nemrég megjelent egy olyan sebességváltó, amelyikben négy bolygómű van, de a bekötések variálásával kilenc (!) előremeneti, s egy hátrameneti áttételt  (fokozatot) lehet kapcsolni. 

 És itt a legmodernebb bolygóműves sebességváltó vázlata!